Навигация
ВЫСШАЯ МАТЕМАТИКА Кривые второго порядка
СОДЕРЖАНИЕ
1 Окружность. Эллипс
2 Гипербола
3 Парабола
4 Литература
1 Окружность. Эллипс
При рассмотрении уравнений прямой на плоскости мы видели, что все они – уравнения первой степени, т. е. переменные х и у входят в них
в первой степени. Рассмотрим основные виды так называемых кривых второго порядка, т. е. кривых, в уравнениях которых переменная х или переменная у, или обе переменные х и у, входят во второй степени, или же входит произведениех·у (степени складываем – получаем тоже вторую степень). Ранее вы уже знакомились с такими уравнениями: ![]() – урав-нение окружности с центром в начале координат радиуса R;
– урав-нение окружности с центром в начале координат радиуса R; ![]() – уравнение гиперболы,
– уравнение гиперболы, ![]() – уравнение параболы. Получим так называемые канонические (основные) уравнения некоторых кривых второго порядка.
– уравнение параболы. Получим так называемые канонические (основные) уравнения некоторых кривых второго порядка.
Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой ее центром. Пусть ![]() – центр
– центр
окружности. R – радиус окружности. Пусть ![]() – произвольная точка окружности. Следовательно,
– произвольная точка окружности. Следовательно, ![]() = =
= = ![]()
![]()
![]() (1)
(1)
(1) – уравнение окружности радиуса R c центром в точке с координатами ![]()
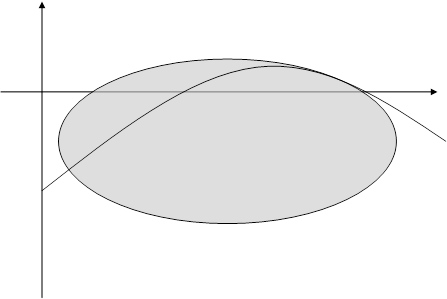
Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек F1 и F2 этой плоскости, называемых фокусами эллипса, есть заданная постоянная величина, равная 2а, а > 0, большая, чем расстояние между фокусами 2с, с > 0.
Пусть фокусы эллипса лежат на оси Х, причем ![]() т. е.
т. е. ![]() – межфокусное расстояние эллипса.
– межфокусное расстояние эллипса.
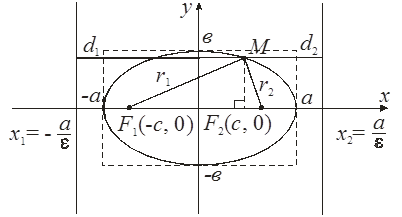
Пусть ![]() – произвольная точка эллипса. Величины
– произвольная точка эллипса. Величины ![]()
![]() называются фокальными радиусами точки М эллипса.
называются фокальными радиусами точки М эллипса.
По определению эллипса: r1 + r2 = 2a, а > c. Из прямоугольных треугольников, по теореме Пифагора, имеем:
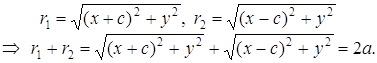 (2)
(2)
Умножим (2) на ![]()
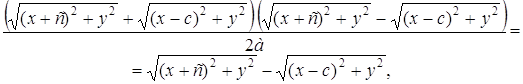
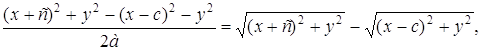
![]() (3)
(3)
Сложим уравнения (2) и (3):
![]()
![]() (4)
(4)
Возведем (4) в квадрат:
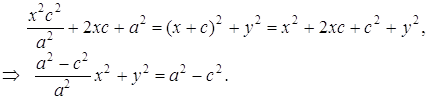
Пусть 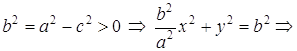
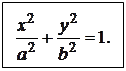
![]() (5)
(5)
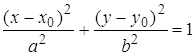 – каноническое уравнение эллипса с центром в точке
– каноническое уравнение эллипса с центром в точке Числа а и ![]() называются соответственно большой и малой полуосями эллипса. Заметим, что а >
называются соответственно большой и малой полуосями эллипса. Заметим, что а > ![]() , если а <
, если а < ![]() , то фокусы эллипса будут на оси Оу, если а =
, то фокусы эллипса будут на оси Оу, если а = ![]() , то эллипс превращается в окружность.
, то эллипс превращается в окружность.
Точки ![]() ,
, ![]() называются вершинами эллипса. Отметим, что эллипс целиком расположен внутри прямоугольника:
называются вершинами эллипса. Отметим, что эллипс целиком расположен внутри прямоугольника: ![]()
Так как ![]()
![]() (6)
(6)
Эксцентриситетом эллипса e называют отношение межфокусного расстояния 2с к длине большой оси 2а.
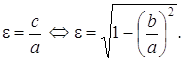 (7)
(7)
Следовательно, ![]() причем
причем ![]() когда
когда ![]() т. е. имеем окружность.
т. е. имеем окружность.
При ![]() стремящемся к 1 эллипс становится более вытянутым вдоль оси Ох.
стремящемся к 1 эллипс становится более вытянутым вдоль оси Ох.
Выразим фокальные радиусы точки ![]() через эксцентриситет. Из (4):
через эксцентриситет. Из (4):
![]() (8)
(8)
Из (3): ![]()
Значит, подставив координаты точки ![]() эллипса в уравнения (8), получаем фокальные радиусы точки М.
эллипса в уравнения (8), получаем фокальные радиусы точки М.
Прямые ![]() называются директрисами эллипса.
называются директрисами эллипса.
![]() – левая директриса,
– левая директриса,
![]() – правая директриса.
– правая директриса.
Заметим, что директрисы эллипса обладают следующим важным свойством:
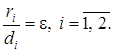 (9)
(9)
т. е. отношение расстояния ri от любой точки эллипса до фокуса к расстоянию di от нее до соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса.
Похожие работы
... Гипербола Две пересекающиеся прямые Гипербола II. Переход от общего уравнения кривой к каноническому Рассмотрим теперь случай, когда, и исследуем данное уравнение кривой второго порядка с помощью инвариантов. Из вышеприведенной таблицы видим, что при уравнение (1) определяет гиперболу и принимает вид: (2.1) Приведем уравнение кривой (2.1) к каноническому виду, ...
... третьего порядка. Яблонский А.И. [11, с.1752 - 1760] и Филипцов В.Ф. [9, с.469-476] изучали квадратичные системы с предположением, что частным интегралом являлись алгебраические кривые четвертого порядка. В данной работе рассматривается система (0.3) и проводится качественное исследование в целом системы (0.3) при условии, что частным интегралом является кривая четвертого порядка, которая ...
... форма j(х) = хТАх была отрицательно определенной, необходимо и достаточно, чтобы ее главные миноры четного порядка были положительны, а нечетного – отрицательны, то есть: М1 < 0, M2 > 0, М3 < 0, …, (–1)n Mn > 0. Пример 3. При каких значениях а и в квадратичная форма будет положительно определенной? j (х1, х2, x3) = Решение. Построим матрицу А и найдем ее главные миноры. ...
... кривой второго порядка и приведя его к каноническому виду, мы установили, что данная кривая — эллипс. Мы получили каноническое уравнение гиперболы при помощи преобразований параллельного переноса и поворота координатных осей. Исследование формы поверхности второго порядка Теоретическая часть Поверхностью второго порядка S называется геометрическое место точек, декартовы прямоугольные ...


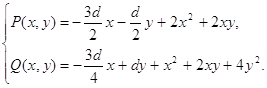
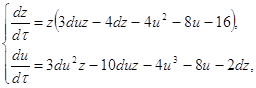


0 комментариев