Навигация
РЕФЕРАТ
з Вищої математики
на тему „Комплексні числа”
1. Комплексні числа
У багатьох розділах математики та її застосуваннях неможливо обмежетись розглядом лише дійсних чисел. Вже досить давно під час розв’язування різних задач виникла потреба добувати квадратний корень з від’їмних чисел. Але чисел, які піднесені до квадрату дають від’ємні числа, тоді не знали і тому вважали, що квадратні корені з від’ємних чисел не існують, тобто задачі, які до них приводять, не мають розв’язків. Зокрема, так було під час розв’язування квадратних рівнянь з від’ємним дискримінантом, наприклад:
х² - 4х + 10 = 0 х₁,₂=2±Ö-6.
Тому природно постало питання про розширення множини дійсних чисел, прєданням до неї нових так, щоб у розширеній множині крім чотирьох арифметичних дій – додавання, віднімання, множення і ділення (за вийнятком ділення на нуль), можна було виконувати дію добування кореня. Це питання було успішно розв’язано лише у ХІХ сторіччі. Відповідно до прийнятих в математиці принципів розширення поняття числа при розширенні множини дійсних чисел мають задовільнятися такі вимоги:
1) озачення нових чисел мусить спиратися на поняття дійсного числа, і нова множина має містити всі дійсні числа;
2) для нових чисел повині виконуватись п’ять законів прямих арифметичних чисел (пригадайте ці закони);
3) у новій числовій множині мусить мати розв’язок рівняння х²=-1.
Оскільки існує вимога, щоб у новій числовій множині рівняння х²=-1 мало розв’язок, необхідно внести деяке нове число, вважаючи його розв’язком цього рівняння. Число, квадрат якого дорівнює –1, позначають буквою і і називають уявною одиницею (і – перша буква латинського слова imaginarius – уявний). Підкреслимо, що рівність і²=-1 приймається за означенням і не доводиться. До нової множини мають належати числа виду bί (добуток дійсного числа на уявну одиницю) і числа виду a + bί (сумма дійсного числа a та добуток дійсного числа b на уявну одиницю).
Отже, нова множина множина чисел повина містити всі числа виду a + bί.Числа виду a + bί, де a і b – довільні дійсні числа, аί – уявна одиниця називають комплексними. Слово “комплексний” означає складений. Число a називають дійсною частиною числа a + bί , а вираз bί – уявною.
Число називають коефіцієнтом при уявній частині. Наприклад, у числі 6 + 7ί дійсна частина 6, уявна 7. Коефіціент при уявній частині дорівнює 7. Дійсною частиною числа 0 + 3ίє число нуль, а уявною – вираз 3ί; коефіцієнт при уявній частині дорівнює 3. Числа виду a + 0ί ототожнюються з дійсними числами, а саме вважають, що a + 0ί=a. Таким чином виконується обов’язкова для будь – якого розширення поняття числа вимога, щоб попередній числовий “запас” входив до нової числової множини як її частина. Множина дійсних чисел є частиною (підмножиною) множини комплексних чисел. Відповідно до вимог, що ставляться при будь – якому розширення поняття числа, при побудові множини комплексних чисел треба ввести за означенням умову рівності цих чисел і правила виконання прямих дій – додавання і множення.
Два комплексних числа a + bί і c + dίрівні між собою тоді і тільки тоді, коли a = c і b=d, тобто коли рівні їх дійсні частини і коефіцієнти при уявних частинах.
Поняття “більше” і “менше” для комплексних чисел не має смислу. Ці числа за величиною не порівнюють. Тому не можна, наприклад, сказати, яке з двох комплексних чисел більше 10ί чи 3ί, 2+5ί чи 5+2ί.
Важливим є поняття про спяжені комплексні числа. Числа a + bί і a - bί, дійсні частини яких рівні, а коефіцієнти при уявих частинах рівні за модулем, але протилежні за знаком, називають спряженими. Можна сказати простіше: числа a + bί і a - bί, які відрізняються лише знаком уявної частини, називають спряженими.
Наприклад, спряженими є комплексні числа 4+3ί та 4-3ί; 2-ί та 2+ί; -8+7ί та –8-7ί;-5-ί та –5+ί. Якщо дане число 6ί, то спряженим до нього є –6ί. До числа 11 спряженим буде 11, бо 11+0ί=11-0ί.
2. Дії над комплексними числами
а) додавання комплексних чисел
Означення: сумою двох комплексних чисел a + bί і c + dί називається комплексне число (a + c) + (b + d)ί, дійсна частина якого і коефіцієнт при уявній частині дорівнюють відповідно сумі дійсних частин і коефіцієнтів при явних частинах додатків, тобто (a + bί) + (c + dί) = (a + c) + (b + d)ί.
Приклади. Виконати додавання комплексних чисел:
1) (3+2ί) + (-1-5ί) = (3-1) + (2-5)ί = 2-3ί
2) (4-5ί) + (2-ί) = (4+2) + (-5-1)ί = 6-6ί
3) (2+3ί) + (6-3ί) = (2+6) + (3-3)ί= 8
4) (10 – 3ί) + (-10+3ί) = (10-10) + (-3+3)ί = 0
З наведених прикладів випливає, що додавання комплексних чисел ми виконуємо за правилом додавання многочленів. У множині дійсних чисел справедлива рівність a + 0 = a. У множині комплексних чисел нулем є число 0 + 0ί. Справді, яке б не було число , справедлива рівність
(a + bί) + (0+0ί) = (a +0) + (b +0)ί = a + bί
За аналогією з дійсними числами, для комплексних чисел вводиться поняття про протилежні числа: два числа a + bί та -a - bί, сумма яких дорівнює 0, називають протилежними.
Додавання комплексних чилел підлягає переставному та сполучному законам. Доведемо, наприклад, справедливість переставного закону додавання комплексних чисел. Нехай,z₁ = a + bί, z₂= c + dί. Тоді z₁+ z₂ = (a + bί) + (c + dί) = (a + c) + (b+d )ί , z₂+ z₁ = (c + dί) + (a + bί) = (c + a) + (d+b)ί. Оскільки для додавання дійсних чисел справджується переставний закон, тобто a + c = c + a; b+d = d+b, тобто (a + c) + (b+d)ί = (c + a) + (d+b)ί , то z₁ + z₂ = z₂+ z₁, що й треба було довести. Означення суми комплексних чисел поширюється і на випадок трьох і більше доданків.
б) віднімання комплексних чисел
Віднімання комплексних чисел означають як дію, обернену до додавання, коли за даною сумою й одним з доданків знаходять другий, невідомий доданок.
Означення. Різницею двох комплексних чисел z₁= a + bί і z₂ = c + dί називається таке комплексне число z₃= x+yί , яке в суммі з z₂ дає z₁.
Отже, z₁- z₂= z₃, якщо z₃ + z₂= z₁. можливість дії віднімання комплексних чисел та її однозначність потребує доведення.
Доведемо, що для будь – яких комплексних чисел z₁= a + bί і z₂ = c + dί різниця z₁- z₂ визначена і до того ж однозначно. Доведемо, що існує, і до того ж єдине, комплексне число z₃= x+yί, яке в сумі з z₂ дає z₁.
За означенням дії віднімання, (c + dί) + (x+yί) = a + bί. виконавши додавання в лівій частині рівності, дістанемо:
(c + x) + (d + y)ί = a + bί (1).
З умови рівності двох комплексних чисел маємо:
c + x = a
d + y = b
Ця система має розвиток, і до того ж єдиний: x = a - c, y = b – d. Отже, існує , і до того ж єдина, пара дійсних чисел (x, y), яка задовільняє рівняння (1), що і треба було довести. З доведеного випливає, що віднімання комплексних чисел виконують за таким правилом:
(a + bί) – (c + dί) = (a - c) + (b – d)ί
Приклади: Виконати віднімання комплексних чисел.
1) (3+4ί) – (1+2ί) = (3-1) + (4-2)ί = 2 + 2ί;
2) (-5+2ί) – (2+ί) = (-5-2) + (2-1)ί = -7+ί;
3) (6+7ί) – (6-5ί) = (6-6) + (7+5)ί = 12ί;
4) (0,3+2,5ί) – (-0,75+1,5ί) = (0,3+0,75ί) + (2,5-1,5ί) = 1,05+ί;
5) (Ö2-2ί) – (Ö2+3ί) = (Ö2-Ö2) + (-2-3)ί = -5ί;
6) 1+1/2) – (1/4-3/5) = (1/3-1/4) + (1/2+3/5) = 1/12 + 11/10.
в) Множення комплексних чисел
Означення. Добутком двох комплексних чисел a + bί і c + dί називається комплексне число (ac - bd) + (ad + bc)ί . Суть і доцільність цьго означення стане зрозумілою, якщо взяти до уваги, що цей добуток утворений так, як виконується множення двочленів з дійсними коефіцієнтами, а саме (a + bί)( c + dί) = ac + adί + bcί + bdί² = ac + (ad + bc)ί + bdί². Замінюючи, за означенням, ί²на –1, дістанемо: bdί² = -bd . Відокремивши дійсну частину від уявної, остаточно матимемо:
(a + bί)( c + dί) = (ac - bd) + (ad + bc)ί (2)
Формулу (2) не слід намагатися механічно запам’ятати. Під час множення комплексних чисел треба користуватись відомим правилом множення двочленів a + bί і c + dί з наступною заміною ί²на –1.
Приклади: Виконити множення комплексних чисел.
1) (4-5ί)(3+2ί) = 12+8ί -15ί -10ί²= 12+10-7ί =22-7ί;
2)(Ö3-ί)(Ö2+Ö5ί) = Ö6-Ö2ί+Ö15ί-Ö5 ί²= (Ö6+Ö5) + (Ö15-Ö2)ί;
3)8ίх3ίхÖ3 = -24Ö3;
4)(2-ί)(-5) = -10+5ί;
5)(-4-3ί)(-6ί) = -18+24ί.
Дія множення комплексних чисел підлягає основним законам множення, встановленим для дійсних чисел: переставному і сполучному.
Знайдемо добуток двох спряжених комплексних чисел. Маємо: (a + bί)( a - bί) = a² - (bί)² = a² -b²ί² = a² + b², тобто (a + bί)( a - bί) = a² + b².
Приклади: Обчислити добуток.
1) (3+5ί)(3-5ί) = 9+25 = 34;
2) (2+ί)(2-ί) = 4+1 = 5;
3) (4+Ö3ί)(4-Ö3ί) = 16+3 = 19;
4) (Öх+Öуί)( Öх-Öуί) = х+у;
5) (3/4+2/5ί)(3/4-2/5ί) = 9/16+4/25 = 289/400.
Читаючи рівність (a + bί)( a - bί) = a² + b² справа наліво, робимо висновок, що сумму квадратів будь – яких двох чисел можна подати у вигляді добутку комплексно – спряжених множників.
Приклади: Розкласти на множники двочлени.
1) а+9 = (а+3ί)(а-3ί);
2) 16m²+25n² = (4m+5nί)(4m-5nί);
3) 49+36 = (7+6ί)(7-6ί);
4) а+16 = (Öа+4ί)( Öа-4ί);
5) в+7 = (Öв+Ö7ί)( Öв-Ö7ί).
г) Ділення комплексних чисел.
Ділення комплексних чисел означають як дію, обернену до дії множення, коли за даним добутком і одним з множників знаходять другий, невідомий множник. Причому в множині комплексних чисел залишається вимога, щоб дільник був відмінним від нуля.
Означення. Часткою комплексних чисел z₁ = a + bί та z₂ = c + dί називеється таке комплексне число z₃= x+yί, яке при множенні на z₂ дає z₁.
Можливість ділення комплексних чисел і його однозначність потребує доведення.
Доведемо, що частка комплексних чисел z₁ = a + bί та z₂ = c + dί визначена і до того ж однозначно, якщо c + dί≠ 0+0ί. Отже, доведемо, що за умови існує, і до того ж єдине, комплексне число z₃= x+yί, яке при множенні на z₂ дає z₁. За означенням дії ділення, (c + dί)( x+yί) = a + bί. Виконавши в лівій частині цієї рівності дію множення, дістанемо: (c x - dy) + (cy +d x)ί = a + bί.
З умови рівності двох комплексних чисел випливає:
c x - dy= a
cy +d x=b
Система має єдиний розв’язок:
x= (a c +bd)\( c²+d²);
y = (bc- ad)\( c²+d²).
Із доведення випливає, що ділення ккомплексних чисел відбувається за таким правилом:
(a + bί)\( c + dί) = (a c +bd)\( c²+d²) + (bc- ad)ί\( c²+d²).
Цей результат можна дістати, помноживши ділене і дільник на число, спряжене до дільника. Покажемо це:
(a + bί)\( c + dί) = (a + bί)( c - dί)\( c + dί)( c - dί) = ((a c +bd) + (bc- ad)ί )\( c²+d²) = (a c +bd)\( c²+d² ) + ((bc- ad)ί)\( c²+d²).
Цим принципом користуються під час розв’язування вправ на ділення комплексних чисел.
Приклади. Знайти частку комплексних чисел.
а) (2+5ί)/(3-2ί) = (2+5ί)(3+2ί)/(3-2ί)(3+2ί) = (-4+19ί)/13 = -4/13+19ί/13;
б) (3+ί)/ί = (3+ί)(-ί)/ί = 1-3ί;
д) піднесення комплексних чисел до степеня.
За означенням, ί¹ = ί, ί²= - 1.
Користуючись рівністю ί²= - 1, визначеко кілька послідовних ступенів уявної одиниці:
ί³ =ί²ί= - 1ί= -ί; ί = ί³ί = -ίί= 1; ί=ίί=ί; ί=ίί=-1; ί=ίί=-ί; ί=-ίί=1.
Оскільки ί=1, то значення степенів періодично повторюються із збільшенням показника на 4. Так, ί²= ί =-1, ί³=ί =-ί, ί =ί = 1і так далі.
Означення. Щоб піднести число до степеня з натуральним показником n, треба показник сепеня поділити на 4 і піднести до степеня, показник якого дорівнює остачі від ділення.
Приклади. Піднести до степеня:
а) ί = ί =ί = ίί =-ί ;
б) ί = ί = ί = ί²= -1;
в) ί =ί = ί = -ί.
Правила піднесення до степеня уявної одиниці застосовується при піднесенні до степеня комплексних чисел.
Приклади. Піднести до степеня двочлени:
1) (2+5ί)² = 4+20ί +25ί² = -21+20ί;
2) (3+2)³ = 27+54ί +36ί²+8 = -9+36ί;
3) (1+ί)² = 1+2ί + ί²= 2ί;
4) (1-ί) ² = 1-2ί + ί²= -2ί;
5) (1-ί) = (1-2ί +ί) ² = (-2ί) ² = 4ί² = -4;
6) (1+ί) = ((1+ί)²)³ = (2ί) ³ = 8ί³ = -8 ί;
7) (1-ί) = ((1-ί) ²) = (-2ί) = -32ί = -32ί.
Рівності(1+ί)² = 1+2ί + ί²= 2ί, (1-ί) ² = 1-2ί + ί²= -2ί корисно запам’ятати, бо їх часто використовують.
Похожие работы
... и ЭДС. В расчёте можно оперировать и действующими значениями величин – ; ; . Символический метод, основанный на изображении векторов комплексными числами введён Штейнмецом, у нас развит ?????????. Связь комплексных амплитуд тока и напряжения в пассивных элементах электрической цепи Законы Кирхгофа для токов и напряжений, представленных комплексными амплитудами ...
... 3. Соглашение о комплексных числах. 1. Действительное число а записывается также в виде a + 0i (или a – 0i). П р и м е р ы. Запись 3 + 0i обозначает то же, что запись 3. Запись –2 + 0i означает –2. 2. Комплексное число вида 0 + bi называется “чисто мнимым”. Запись bi обозначает то же, что 0 + bi. 3. Два комплекных a + bi, a’ + b’i считаются равными ...
... учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала ...
... 1. Точки М и N — середины диагоналей АС и BD четырехугольника ABCD. (Рис.1)Доказать, что |AB|2+|BC|2+|CD|2+|DA|2 = |AC|2+|BD|2+4|MN|2.Решение. Пусть точкам A, В, С, D, М, N соответствуют комплексные числа а, b, с, d, т, п.Так как m = и n = , то |AB|2+|BC|2+|CD|2+|DA|2 |AC|2+|BD|2+4|MN|2 .Равенство доказано.Задача 2. Доказать, что если в плоскости параллелограмма ABCD существует такая точка М, ...
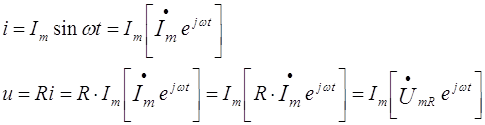
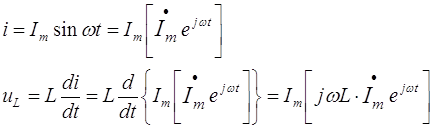
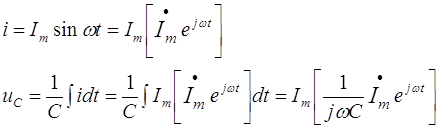
0 комментариев