Навигация
Содержание
Введение........................................................................................................... 3
§1. Основные понятия и определения............................................................. 4
1.1. Линейные пространства........................................................................... 4
1.2. Нормированные пространства................................................................ 5
1.3. Банаховы пространства............................................................................ 6
1.4. Компактные множества............................................................................ 8
1.5. Линейные операторы и линейные функционалы.................................. 11
1.6. Сопряженные операторы....................................................................... 12
§2. Компактные операторы........................................................................... 13
2.1. Определение компактного оператора................................................... 13
2.2. Свойства компактных операторов......................................................... 13
2.3. Примеры некомпактного и компактных операторов........................... 16
Литература..................................................................................................... 20
Введение
Изучение произвольных линейных операторов представляет собой весьма трудоемкую задачу, однако среди линейных операторов можно выделить классы операторов, которые могут быть рассмотрены более подробно. Данная работа рассматривает основные понятия, свойства, определения и теоремы, связанные с одним из классов линейных операторов – компактными операторами.
Работа состоит из двух параграфов. Первый из них содержит предварительные сведения, необходимые для рассмотрения темы: понятия пространств, которые необходимы при изучении компактных операторов, понятия линейного оператора и линейного функционала, сопряженного оператора, компактного множества. Во втором параграфе рассмотрено определение компактного оператора, основные свойства этого класса операторов и примеры компактных и некомпактного оператора.
§1. Основные понятия и определения.
1.1 Линейные пространства.
Определение: Непустое множество ![]() элементов называется линейным, если оно удовлетворяет таким условиям:
элементов называется линейным, если оно удовлетворяет таким условиям:
I. ![]() Для любых двух элементов
Для любых двух элементов ![]() определен единственный элемент
определен единственный элемент ![]() , называемый суммой и обозначаемый
, называемый суммой и обозначаемый ![]() , причем
, причем
1) ![]() ;
;
2) ![]() ;
;
3) в ![]() существует такой элемент 0, что
существует такой элемент 0, что ![]() для всех
для всех ![]() ;
;
4) для каждого ![]() существует такой элемент
существует такой элемент ![]() , что
, что ![]() .
.
II. Для любого числа ![]() и любого элемента
и любого элемента ![]() определен элемент
определен элемент ![]() , причем
, причем
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
([1], стр. 120).
Примеры линейных пространств
1. Пространство действительных чисел ![]() является линейным пространством по операциям сложения и умножения.
является линейным пространством по операциям сложения и умножения.
2. ![]() – пространство, элементами которого являются последовательности чисел
– пространство, элементами которого являются последовательности чисел ![]() , удовлетворяющих условию
, удовлетворяющих условию 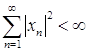 с операциями
с операциями ![]() ,
, ![]()
([1], стр. 121).
Похожие работы
... состоит из значений функции g(x) на отрезке [a,b]. Причём этот оператор имеет лишь непрерывный спектр, так как резольвента при существует, но не непрерывна. Точечного спектра оператор не имеет. Пример 3: Рассмотрим оператор дифференцирования на множестве дифференцируемых функций. А: (для краткости будем писать вместо f(x) просто f). Рассмотрим резольвенту этого оператора: , то есть мы должны ...
... : µ§. Шары такие : µ§ и µ§, причем: µ§ , µ§. µ§ µ§ Если µ§ ,то: µ§ , µ§ µ§ µ§ µ§ µ§ Теорема доказана. Единственность классического решения задачи Дирихле для уравнения Пуассона. µ§ µ§ (1) µ§ µ§ (2) µ§ - это не гарантирует существование решения. µ§ Теорема. Задача (1) (2) может иметь не более одного ...
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА = ...
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА ...


0 комментариев