Кафедра: Автоматика и информационные технологии
"ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ"
Екатеринбург 2006
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ ПРОСТОЙ ИТЕРАЦИИ
Одной из самых распространенных и важных задач вычислительной математики является решение системы линейных алгебраических уравнений (СЛАУ):
a11 x1 + a12 x2 + … + a1n xn = b1
a21 x1 + a22 x2 + … + a21 xn = b2
……………………………………. .
an1 x1 + an1 x2 +… + ann xn = bn,
или в векторно-матричном виде:
Ax = B, (1)
![]() где
где
![]()
![]() а11 а12 ......а1n
а11 а12 ......а1n
а21 а22 -… .. а2n
А = ................
![]() аn1 аn2 … . ann
аn1 аn2 … . ann
![]() b1
b1 ![]()
b2
B =
![]() bn
bn
![]() x1
x1 ![]()
x2
x =
![]() xn
xn
Итерационные методы решения СЛАУ используются для решения СЛАУ большой размерности с разреженными матрицами, а также для уточнения решения СЛАУ, полученного с помощью прямого метода. Формулировка и применение итерационных методов требует определенных знаний и определенного опыта. Выбор эффективного итерационного метода решения конкретной задачи существенно зависит от ее характерных свойств и от архитектуры вычислительной машины, на которой будет решаться задача. Поэтому никаких общих правил выбора наилучшего итерационного метода решения не существует. Метод простой итерации приведен здесь как иллюстрация действия механизма вычисления решения на основе итерационной процедуры.
Суть метода состоит в следующем. От системы уравнений вида Ах = в (2) переходят к системе уравнений
x=Dх + С (3)
Например, от системы уравнений
а11х1+а12х2+а13х3=в1
а21х1+а22х2+а23х3=в2 (4)
а31х1+а32х2+а33х3=в3
можно перейти к виду (3), выразив из первого уравнения х1, из второго - х2, из третьего - х3:
х1= - а12/а11х2 - а13/а11х3+в1/а11
х2= - а21/а22х1 - а23/а22х3+в2/а22 (5)
х3= - а31/а33х1 - а32/а33х2+ в3/а33
Приведение исходной системы уравнений в виду (3) можно осуществить различными способами. Например, в СЛАУ (4) из первого уравнения можно выразить х2, из второго - х1, из третьего - х3 и, переставив уравнения для сохранения порядка следования переменных в векторе решения х, снова прийти к виду (3). Естественно, что матрица D и вектор с будут уже иными. Возможны и другие способы преобразования исходных уравнений.
После преобразования (2) к виду (3) назначается нулевое приближение решения х (0):
 х1 (0)
х1 (0)
х (0) = х2 (0)
х3 (0).
Если приблизительно известны значения хi вектора решения х, то они выбираются в качестве нулевого приближения, если нет, то в качестве вектора х (0) выбирается любой вектор, например х (0) =С.
Первый шаг итерационного процесса состоит в вычислении приближения х (1):
х (1) = Dx (0) +С.
Например, назначив х (0) и подставив его в систему уравнений (3), получим:
х1 (1) = - а12/а11х (0) - а13/а11х3 (0) +в1/а11
х2 (1) = - а21/а22х1 (0) - а23/а22х3 (0) +в2/а22
х3 (0) = - а31/а33х1 (0) - а32/а33х2 (0) +в3/а33.
Далее вычисляем:
х (2) = Dx (1) +C
х (к) =Dх (к-1) +С
и т.д.
Достаточное условие сходимости метода итерации заключается в следующем, если норма матрицы D (обозначается ║D║) меньше 1, то система уравнений (3) имеет единственное решение х* и итерации сходятся к этому решению со скоростью геометрической прогрессии Иными словами, если
║D║<1, (6)
то
ℓim ║х (к) - х*║= 0
к→∞
и выполняется тождество
х*=Dх*+С.
В качестве нормы матрицы D используются нормы ║D║1 или
║D║∞: n
║D║1 = max ∑ | dij |,
j i=1
n
║D║∞= max ∑ | dij |.
i j=1
![]() Аналогично вводятся нормы вектора х:
Аналогично вводятся нормы вектора х:
n
║х║1 = ∑ |хi|
i=1
║х║∞= max |xi|.
i
Из условия сходимости (6) ясно, что не всякое преобразование исходной системы (2) к виду (3) позволит получить решение уравнения на основе итерационного процесса, а только такое, которое обеспечит выполнение условия ║D║<1. Важно иметь в виду, что при выполнении этого условия итерационный процесс сходится для любого начального приближения х (0) и выбор х (0) =С диктуется просто соображениями удобства назначения х (0).
Если задана допустимая погрешность вычислений Δ, то для оценки погрешности к - го приближения широко используется следующее неравенство:
║х (к) - х*║≤║D║ ∕ (1-║D║) •║х (к) - х (к-1) ║<Δ (7)
Из этого неравенства следует критерий окончания итерационного процесса
║х (к) - х (к-1) ║ < (1-║ D║) •∆ ∕ ║D║ (8)
Каждый раз при вычислении очередного приближения х (k) проверяется выполнение неравенства (8).
Выполнение неравенства (8) означает выполнение неравенства
║х (к) - х*║ < ∆
и, следовательно, прекращение итерационного процесса.
ЗАДАНИЕ НА ВЫПОЛНЕНИЕ РАБОТЫ
Проверить выполнение условия сходимости итерационного процесса.
Найти решение СЛАУ, задавая различные значения вектора начального приближения к решению x (0) и фиксируя количество итераций, необходимых для достижения решения с заданной точностью.
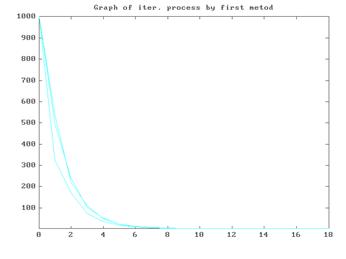
Построить графики xi (k),i=1,n решения в зависимости от номера итерации k.
Варианты заданий к теме "Решение СЛАУ методом итераций"
| № варианта | D | C | ||||
| 1 | 0.23 | -0.04 | 0.21 | -0.18 | 1.24 | |
| 0.45 | -0.23 | 0.06 | 0.00 | -0.88 | ||
| 0.26 | 0.34 | -0.11 | 0.00 | 0.62 | ||
| 0.05 | -0.26 | 0.34 | -0.12 | -1.17 | ||
| 2 | 0.21 | 0.12 | -0.34 | -0.15 | -0.64 | |
| 0.34 | -0.08 | 0.17 | -0.18 | 1.42 | ||
| 0.16 | 0.34 | 0.15 | -0.31 | -0.42 | ||
| 0.12 | -0.25 | -0.08 | 0.25 | 0.83 | ||
| 3 | 0.32 | -0.18 | 0.02 | 0.21 | 1.83 | |
| 0.16 | 0.12 | -0.14 | 0.27 | 0.65 | ||
| 0.37 | 0.27 | -0.02 | -0.24 | 2.23 | ||
| 0.12 | 0.21 | -0.18 | 0.25 | -0.13 | ||
| 4 | 0.42 | -0.52 | 0.03 | 0.00 | 0.44 | |
| 0.31 | -0.25 | -0.36 | 0.00 | 1.42 | ||
| 0.10 | 0.08 | -0.14 | -0.24 | -0.83 | ||
| 0.15 | -0.35 | -0.18 | 0.00 | -1.42 | ||
| 5 | 0.18 | -0.34 | -0.12 | 0.15 | -1.33 | |
| 0.11 | 0.23 | -0.45 | 0.32 | 0.84 | ||
| 0.05 | -0.12 | 0.14 | -0.18 | -1.16 | ||
| 0.12 | 0.08 | 0.06 | 0.00 | 0.57 | ||
| 6 | 0.13 | 0.23 | -0.44 | -0.05 | 2.13 | |
| 0.24 | 0.00 | -0.31 | 0.15 | -0.18 | ||
| 0.06 | 0.15 | 0.00 | -0.23 | 1.44 | ||
| 0.52 | -0.08 | -0.05 | 0.00 | 2.42 | ||
| 7 | 0.17 | 0.31 | -0.18 | 0.22 | -1.71 | |
| -0.21 | 0.00 | 0.33 | 0.22 | 0.62 | ||
| 0.32 | -0.18 | 0.05 | -0.19 | -0.89 | ||
| 0.12 | 0.28 | -0.14 | 0.00 | 0.94 | ||
| 8 | 0.13 | 0.27 | -0.22 | -0.18 | 1.21 | |
| -0.21 | 0.00 | -0.35 | 0.18 | -0.33 | ||
| 0.12 | 0.13 | -0.33 | 0.10 | -0.48 | ||
| 0.33 | -0.05 | 0.05 | -0.28 | -0.17 | ||
Варианты заданий к теме "Решение СЛАУ методом итераций"
| № варианта | D | C | ||||
| 9 | 0.19 | -0.07 | 0.38 | -0.21 | -0.81 | |
| -0.22 | 0.08 | 0.11 | 0.33 | -0.64 | ||
| 0.51 | -0.07 | 0.09 | -0.11 | 1.71 | ||
| 0.33 | -0.41 | 0.00 | 0.00 | -1.21 | ||
| 10 | 0.00 | 0.22 | -0.11 | 0.31 | 2.70 | |
| 0.38 | 0.00 | -0.12 | 0.22 | -1.50 | ||
| 0.11 | 0.23 | 0.00 | -0.51 | 1.20 | ||
| 0.17 | -0.21 | 0.31 | 0.00 | -0.17 | ||
| 11 | 0.07 | -0.08 | 0.11 | -0.18 | -0.51 | |
| 0.18 | 0.52 | 0.00 | 0.21 | 1.17 | ||
| 0.13 | 0.31 | 0.00 | -0.21 | -1.02 | ||
| 0.08 | 0.00 | -0.33 | 0.28 | -0.28 | ||
| 12 | 0.05 | -0.06 | -0.12 | 0.14 | -2.17 | |
| 0.04 | -0.12 | 0.68 | 0.11 | 1.40 | ||
| 0.34 | 0.06 | -0.06 | 0.44 | -2.10 | ||
| 0.11 | 0.12 | 0.00 | -0.03 | -0.80 | ||
| 13 | 0.08 | -0.03 | 0.00 | -0.04 | -1.20 | |
| 0.00 | 0.51 | 0.27 | -0.08 | 0.81 | ||
| 0.33 | -0.37 | 0.00 | 0.21 | -0.92 | ||
| 0.11 | 0.00 | 0.03 | 0.58 | 0.17 | ||
| 14 | 0.12 | -0.23 | 0.25 | -0.16 | 1.24 | |
| 0.14 | 0.34 | -0.18 | 0.24 | -0.89 | ||
| 0.33 | 0.03 | 0.48 | -0.32 | 1.15 | ||
| 0.12 | -0.05 | 0.00 | 0.15 | -0.57 | ||
| 15 | 0.23 | -0.14 | 0.06 | -0.12 | 1.21 | |
| 0.12 | 0.00 | 0.32 | -0.18 | -0.72 | ||
| 0.08 | -0.12 | 0.23 | 0.32 | -0.58 | ||
| 0.25 | 0.22 | 0.14 | 0.00 | 1.60 | ||
| 16 | 0.14 | 0.23 | 0.18 | 0.17 | -1.42 | |
| 0.12 | -0.14 | 0.08 | 0.09 | -0.83 | ||
| 0.16 | 0.24 | 0.00 | -0.35 | 1.21 | ||
| 0.23 | -0.08 | 0.55 | 0.25 | 0.65 | ||
Варианты заданий к теме "Решение СЛАУ методом итераций"
| № варианта | D | C | ||||
| 17 | 0.24 | 0.21 | 0.06 | -0.34 | 1.42 | |
| 0.05 | 0.00 | 0.32 | 0.12 | -0.57 | ||
| 0.35 | -0.27 | 0.00 | -0.05 | 0.68 | ||
| 0.12 | -0.43 | 0.34 | -0.21 | -2.14 | ||
| 18 | 0.17 | 0.27 | -0.13 | -0.11 | -1.42 | |
| 0.13 | -0.12 | 0.09 | -0.06 | 0.48 | ||
| 0.11 | 0.05 | -0.02 | 0.12 | -2.34 | ||
| 0.13 | 0.18 | 0.24 | 0.43 | 0.72 | ||
| 19 | 0.00 | 0.28 | -0.17 | 0.06 | 0.21 | |
| 0.52 | 0.00 | 0.12 | 0.17 | -1.17 | ||
| 0.17 | -0.18 | 0.21 | 0.00 | -0.81 | ||
| 0.11 | 0.22 | 0.03 | 0.05 | 0.72 | ||
| 20 | 0.15 | 0.05 | -0.08 | 0.14 | -0.48 | |
| 0.32 | -0.43 | -0.12 | 0.11 | 1.24 | ||
| 0.17 | 0.06 | -0.08 | 0.12 | 1.15 | ||
| 0.21 | -0.16 | 0.36 | 0.00 | -0.88 | ||
| 21 | 0.00 | 0.52 | 0.08 | 0.13 | -0.22 | |
| 0.07 | -0.38 | -0.05 | 0.41 | 1.80 | ||
| 0.04 | 0.42 | 0.11 | -0.07 | -1.30 | ||
| 0.17 | 0.18 | -0.13 | 0.19 | 0.33 | ||
| 22 | 0.00 | 0.17 | -0.33 | 0.18 | -1.20 | |
| 0.00 | 0.18 | 0.43 | -0.08 | 0.33 | ||
| 0.22 | 0.18 | 0.21 | 0.07 | 0.48 | ||
| 0.08 | 0.07 | 0.71 | 0.04 | -1.20 | ||
| 23 | 0.01 | 0.02 | -0.62 | 0.08 | -1.30 | |
| 0.03 | 0.28 | 0.33 | -0.07 | 1.10 | ||
| 0.09 | 0.13 | 0.42 | 0.28 | -1.70 | ||
| 0.19 | -0.23 | 0.08 | 0.37 | 1.50 | ||
| 24 | 0.03 | -0.05 | 0.22 | -0.33 | 0.43 | |
| 0.22 | 0.55 | -0.88 | 0.07 | -1.80 | ||
| 0.33 | 0.13 | -0.08 | -0.05 | -0.80 | ||
| 0.08 | 0.17 | 0.29 | 0.33 | 1.70 | ||
Варианты заданий к теме "Решение СЛАУ методом итераций"
| № варианта | D | C | ||||
| 25 | 0.13 | 0.22 | -0.33 | 0.07 | 0.11 | |
| 0.00 | 0.45 | -0.23 | 0.07 | -0.33 | ||
| 0.11 | 0.00 | -0.08 | 0.78 | 0.85 | ||
| 0.08 | 0.09 | 0.33 | 0.21 | -1.70 | ||
| 26 | 0.32 | -0.16 | -0.08 | 0.15 | 2.42 | |
| 0.16 | -0.23 | 0.11 | -0.21 | 1.43 | ||
| 0.05 | -0.08 | 0.00 | 0.34 | -0.16 | ||
| 0.12 | 0.14 | -0.18 | 0.06 | 1.62 | ||
| 27 | 0.00 | 0.08 | -0.23 | 0.32 | 1.34 | |
| 0.16 | -0.23 | 0.18 | 0.16 | -2.33 | ||
| 0.15 | 0.12 | 0.32 | -0.18 | 0.34 | ||
| 0.25 | 0.21 | -0.16 | 0.03 | 0.63 | ||
| 28 | 0.06 | 0.18 | 0.33 | 0.16 | 2.33 | |
| 0.32 | 0.00 | 0.23 | -0.35 | -1.12 | ||
| 0.16 | -0.08 | 0.00 | -0.12 | 0.43 | ||
| 0.09 | 0.22 | -0.13 | 0.00 | 0.83 | ||
| 29 | 0.00 | 0.34 | 0.23 | -0.06 | 1.42 | |
| 0.11 | -0.23 | -0.18 | 0.36 | -0.66 | ||
| 0.23 | -0.12 | 0.16 | -0.35 | 1.08 | ||
| 0.12 | 0.12 | -0.43 | 0.18 | 1.72 | ||
| 30 | 0.32 | -0.23 | 0.41 | -0.06 | 0.67 | |
| 0.18 | 0.12 | -0.33 | 0.00 | -0.88 | ||
| 0.12 | 0.32 | -0.35 | 0.67 | -0.18 | ||
| 0.05 | -0.11 | 0.09 | -0.12 | 1.44 | ||
Список литературы
1. Вержбицкий В.М. Основы численных методов: Учебник для вузов. - М.: Высш. шк., 2002. - 840с.
2. Волков Е.А. Численные методы: Учебное пособие. - 3-е изд., испр. - СПб: Лань, 2004. - 248с.
3. Кетков Ю.Л. MATLAB 6: программирование численных методов. - СПб.: БВХ-Петербург, 2004. - 672с.
4. Турчак Л.И. Основы численных методов: Учебное пособие. - М.: Наука. Гл. ред. физ. - мат. лит., 1987. - 320с.
5. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ: Методические указания к лабораторной работе по дисциплине "Вычислительная математика"/сост. И.А. Селиванова. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2006. - 12 с.
6. Указания предназначены для студентов всех форм обучения специальности 230101 - "Вычислительные машины, комплексы, системы и сети" и бакалавров направления 230100 - "Информатика и вычислительная техника".
Похожие работы
... конкретной задаче (анализ) Составляя задачи на языке программирования Borland C++ Builder 6 для реализации точных методов решения СЛАУ я учитывал разное количество уравнений в системе (размерность матрицы задавал равным nxn). Но для проверки результатов использовал систему уравнений: Вообще говоря, процесс Зейделя сходится быстрее, чем метод Якоби. Бывает, что процесс Зейделя сходится, ...
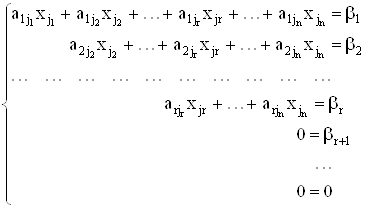
... образом, исходная система может быть представлена в виде: , откуда получаем: x =1, y = 2, z = 3. 2. Математические и алгоритмические основы решения задачи 2.1 Описание метода Метод Гаусса - классический метод решения системы линейных алгебраических уравнений (СЛАУ). Состоит в постепенном понижении порядка системы и исключении неизвестных. Пусть исходная система выглядит следующим ...
... матрицы могут вычисляться по следующим формулам: 6. Метод квадратного корня Использование разложения на взаимно транспонированные треугольные матрицы при решении систем алгебраических уравнений называется метод квадратного корня. Метод разложения на транспонированные треугольные матрицы имеет модификацию, заключающуюся в выделении в произведении диагональной матрицы D с элементами на ...
... , но выбор перехода к системе x=(x) зависит от типа конкретной решаемой системы линейных алгебраических уравнений. 6. Заключение В данной курсовой работе был реализован метод простой итерации для решения систем линейных алгебраических уравнений в виде двух программ, каждая из которых использует свой собственный способ перехода от системы вида F(x)=x к системе вида x=(x). Вообще говоря, ...
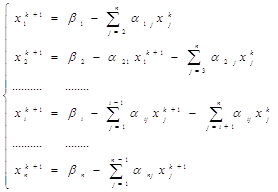



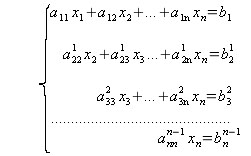



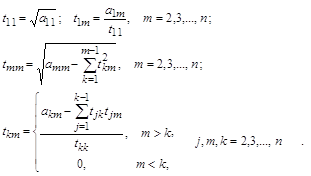
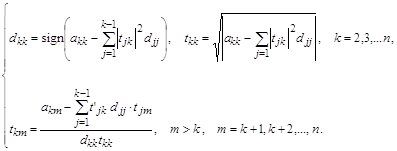



0 комментариев