Министерство образования и науки Украины
Днепропетровский Национальный Университет
Факультет электроники, телекоммуникаций и компьютерных систем
Кафедра АСОИ
Расчётная задача №2
«Исследование операций»
Выполнил:
Ст. группы РС-05
Проверил:
Доцент кафедры АСОИ
Саликов В.А.
г. Днепропетровск
2007г.
Условие задачи
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1)Решим графическим методом
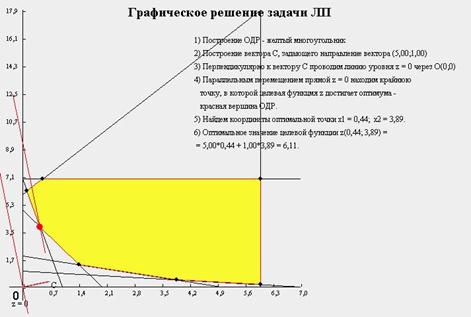
Следовательно, оптимальное решение: X1=4/9
Х2=35/9
Минимальное значение целевой функции: Z=55/9
2)Симплекс-метод
В случае, когда одно или несколько ограничений имеют знаки ³ или = невозможно получить решение. Для получения начального допустимого базиса вводят искусственные переменные R1,R2,R3,R4. Поскольку R1,R2,R3,R4 не имеют отношение к содержательной постановке задачи, то за их применение назначается штраф. В ходе решения задачи на заключительной итерации эти переменные должны принять нулевое значение и выйти из базиса.
Симплексный метод решения задачи линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план, и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какой-нибудь исходный опорный план.
Приведем задачу к каноническому виду:Z=5x1+x2 min
Добавим в систему уравнений искусственные переменные R
![]()
при ограничениях:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
x1 >= 0; x2 >= 0; x3 >= 0; x4 >= 0; x5 >= 0; x6 >= 0; x7 >= 0; x8 >= 0; x9 >= 0; R1 >= 0; R2 >= 0; R3 >= 0; R4 >= 0
Существуют базисные и небазисные переменные.
Включающиеся переменные называются небазисными в данный момент переменными, которые включаются в состав базиса на следующей итерации.
Исключаемые - базисные переменные, которые на следующей итерации подлежат исключению.
На следующем шаге необходимо подставить значение ![]() в целевую функцию:
в целевую функцию:
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, задача в стандартной форме имеет следующий вид:
![]()
x1 >= 0; x2 >= 0; x3 >= 0; x4 >= 0; x5 >= 0; x6 >= 0; x7 >= 0; x8 >= 0; x9 >= 0; R1 >= 0; R2 >= 0; R3 >= 0; R4 >= 0
Перенесем члены целевой функции влево
z -5x1-1x2 = 0
Далее задача решается обычным симплекс-методом
Шаг 0. Используя линейную модель стандартной формы, определяют начальное допустимое базисное решение путем приравнивания к нулю n- m небазисных переменных.
Шаг 1. Из числа небазисных переменных (равных нулю) выбирается включаемая в новый базис переменная, увеличение которой обеспечивает больший по сравнению с остальными рост целевой функции (условие оптимальности). Если такой переменной нет, вычисления прекращаются и полученное решение является оптимальным. В противном случае, переходят к шагу 2.
Шаг 2. Из числа переменных текущего базиса выбирается исключаемая переменная, значение которой быстрее всех стремится к нулю при переходе к новой смежной точке (становящаяся небазисной и равной нулю при введении в базис новой переменной - условие допустимости).
Шаг 3. Определяется новое базисное решение (соответствующее новой смежной точке, т.е. новому составу базисных и небазисных переменных) и осуществляется переход к шагу 1.
Строим симплекс таблицу:
| Базис |
|
|
|
|
|
|
|
|
|
|
|
|
| Решение | Оценка |
| Z |
|
|
| 0 |
|
|
| 0 | 0 | 0 | 0 | 0 | 0 |
| |
|
| -2 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 6 |
|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 6 | - |
|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 7 | 7 |
|
| 1 | 7 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 7 | 1 |
|
| 2 | 5 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 10 | 2 |
|
| 5 | 2 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 10 | 5 |
|
| 7 | 1 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 1 | 7 | 7 |
![]() - ведущий столбец
- ведущий столбец
![]() - ведущая строка
- ведущая строка
Из числа текущих небазисных переменных выбирается включаемая в новый базис переменная, увеличение которой обеспечивает улучшение целевой функции
Для определения нового базисного решения (шаг 3) воспользуемся методом Гаусса-Жордана:
А) новая ведущая строка = предыдущая ведущая строка / ведущий элемент;
Б) новое уравнение = предыдущему уравнению – {старый коэффициент ведущего столбца, соответствующий искомому уравнению * новую ведущую строку}
Новая симплекс – таблица будет иметь следующий вид:
| Базис |
|
|
|
|
|
|
|
|
|
|
|
|
| Решение | Оценка |
| Z |
| 0 |
| 0 |
|
|
| 0 | 0 |
| 0 | 0 | 0 |
| |
|
|
| 0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | - |
|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 6 | 6 |
|
|
| 0 |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 6 | - |
|
|
| 1 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 7 |
|
|
| 0 |
| 0 | -1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 5 |
|
|
|
| 0 |
| 0 | 0 | -1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 8 |
|
|
|
| 0 |
| 0 | 0 | 0 | -1 | 0 | 0 |
| 0 | 0 | 1 | 6 |
|
![]() - ведущий столбец
- ведущий столбец
![]() - ведущая строка
- ведущая строка
В столбцах векторов, входящих в базис, на пересечении строк и столбцов одноименных векторов проставляются единицы, а все остальные элементы данных столбцов полагают равными нулю.
В состав таблицы входят столбцы для базисных переменных и всех переменных, входящих в целевую функцию и ограничения, и, кроме того, столбец решений и отношений. Строками таблицы являются строки из коэффициентов при переменных в соответствующих уравнениях для базисных переменных.
Для решения задачи шага 1 из числа небазисных (равных нулю) переменных выбираем включаемую переменную, имеющую наибольший отрицательный коэффициент в z – уравнении (условие оптимальности), т.к. при этом обеспечивается максимальный прирост целевой функции в стандартной форме. Столбец с включаемой переменной становится ведущим.
Исключаемую переменную (шаг 2) определяем по минимальному положительному отношению правой части уравнения к соответствующему коэффициенту ведущего столбца (условие допустимости - обращение в нуль данной переменной в смежной точке). Строка, соответствующая исключаемой переменной, становится ведущей. Далее определяем ведущий элемент таблицы на пересечении ведущего столбца и строки
Во вводимой переменной в задаче минимизации является небазисная переменная, имеющая в Z-уравнении наибольший положительный коэффициент.
| Базис |
|
|
|
|
|
|
|
|
|
|
|
|
| Решение | Оценка |
| Z | 0 | 0 |
| 0 |
|
|
| 0 | 0 |
| 0 | 0 |
|
| |
|
| 0 | 0 |
| 1 | 0 | 0 |
| 0 | 0 |
| 0 | 0 |
|
|
|
|
| 0 | 0 |
| 0 | 0 | 0 |
| 1 | 0 |
| 0 | 0 |
|
| - |
|
| 0 | 0 |
| 0 | 0 | 0 |
| 0 | 1 |
| 0 | 0 |
|
| 42 |
|
| 0 | 1 |
| 0 | 0 | 0 |
| 0 | 0 |
| 0 | 0 |
|
| - |
|
| 0 | 0 |
| 0 | -1 | 0 |
| 0 | 0 |
| 1 | 0 |
|
|
|
|
| 0 | 0 |
| 0 | 0 | -1 |
| 0 | 0 |
| 0 | 1 |
|
|
|
|
| 1 | 0 |
| 0 | 0 | 0 |
| 0 | 0 |
| 0 | 0 |
|
| 42 |
![]() - ведущий столбец
- ведущий столбец
![]() - ведущая строка
- ведущая строка
Базис |
|
|
|
|
|
|
|
|
|
|
|
|
| Решение | Оценка |
| Z | 0 | 0 | 0 | 0 |
|
|
| 0 | 0 |
|
| 0 |
|
| |
|
| 0 | 0 | 0 | 1 |
| 0 |
| 0 | 0 | 0 |
| 0 |
|
| - |
|
| 0 | 0 | 0 | 0 |
| 0 |
| 1 | 0 | 0 |
| 0 |
|
|
|
|
| 0 | 0 | 0 | 0 |
| 0 |
| 0 | 1 | 0 |
| 0 |
|
| - |
|
| 0 | 1 | 0 | 0 |
| 0 |
| 0 | 0 | 0 |
| 0 |
|
| 28 |
|
| 0 | 0 | 1 | 0 |
| 0 |
| 0 | 0 | -1 |
| 0 |
|
|
|
|
| 0 | 0 | 0 | 0 |
| -1 |
| 0 | 0 | 0 |
| 1 |
|
|
|
|
| 1 | 0 | 0 | 0 |
| 0 |
| 0 | 0 | 0 |
| 0 |
|
| - |
![]() - ведущий столбец
- ведущий столбец
![]() - ведущая строка
- ведущая строка
Базис |
|
|
|
|
|
|
|
|
|
|
|
|
| Решение | Оценка |
| Z | 0 | 0 | 0 | 0 |
|
| 0 | 0 | 0 |
|
|
|
|
| |
|
| 0 | 0 | 0 | 1 |
|
| 0 | 0 | 0 | 0 |
|
| 0 |
|
|
|
| 0 | 0 | 0 | 0 |
|
| 0 | 1 | 0 | 0 |
|
| 0 |
| - |
|
| 0 | 0 | 0 | 0 |
|
| 0 | 0 | 1 | 0 |
|
| 0 |
|
|
|
| 0 | 1 | 0 | 0 |
|
| 0 | 0 | 0 | 0 |
|
| 0 |
| - |
|
| 0 | 0 | 1 | 0 |
|
| 0 | 0 | 0 | -1 |
|
| 0 |
| - |
|
| 0 | 0 | 0 | 0 |
|
| 1 | 0 | 0 | 0 |
|
| -1 |
|
|
|
| 1 | 0 | 0 | 0 |
|
| 0 | 0 | 0 | 0 |
|
| 0 |
| 15 |
![]() - ведущий столбец
- ведущий столбец
![]() - ведущая строка
- ведущая строка
Базис |
|
|
|
|
|
|
|
|
|
|
|
|
| Решение |
| Z | 0 | 0 | 0 | 0 | 0 |
|
| 0 | 0 |
|
|
|
|
|
|
| 0 | 0 | 0 | 1 | 0 | 1 | -1 | 0 | 0 | 0 | 0 | -1 | 1 | 3 |
|
| 0 | 0 | 0 | 0 | 0 |
|
| 1 | 0 | 0 | 0 |
|
|
|
|
| 0 | 0 | 0 | 0 | 0 |
|
| 0 | 1 | 0 | 0 |
|
|
|
|
| 0 | 1 | 0 | 0 | 0 |
|
| 0 | 0 | 0 | 0 |
|
|
|
|
| 0 | 0 | 1 | 0 | 0 |
|
| 0 | 0 | -1 | 0 |
|
|
|
|
| 0 | 0 | 0 | 0 | 1 |
|
| 0 | 0 | 0 | -1 |
|
|
|
|
| 1 | 0 | 0 | 0 | 0 |
|
| 0 | 0 | 0 | 0 |
|
|
|
Если переменной для включения в базис нет и все коэффициенты при небазисных переменных - отрицательны, то полученное решение оптимально.
Таким образом, оптимальное решение задачи имеет вид:
![]()
![]() ,
, ![]()
Так как, значение целевой функции, вычисленное симплекс методом, совпало со значением, полученным в результате решения графическим методом, можно сделать вывод, что найденные значения ![]() верны.
верны.
Похожие работы
... , 6) сетевого планирования и управления, 7) выбора маршрута, 8) комбинированные. Из перечисленных выше методов математического программирования наиболее развитым и законченным является линейное программирование. В его рамки укладывается широкий круг задач исследования операций. Линейное программирование Несмотря на требование линейности целевой функции и ограничений, в рамки линейного ...
... -бухгалтер должен: а) потребовать недостающие материалы у проверяемой организации; б) составить сообщение о невозможности дачи заключения; в) заявить письменное ходатайство о предоставлении ему дополнительных документов. 1. Исследование операций по заработной плате Задачей судебно-бухгалтерской экспертизы при исследовании операций по труду и заработной плате является активизация ...
... и направление ветра, плотность воздуха и др. 4. Эквифинальность. Рано или поздно, самолет вынужден будет приземлится или разобьется. Т.о. скорости, ускорения, моменты и силы будут равны нулю. Исследование операций Задача 1 Авиакомпания «Небесный грузовик», обслуживающая периферийные районы страны, располагает А1 самолетами типа 1, А2 самолетами типа 2, А3 самолетами типа 3, которые она ...
... Лагранжа: L(x,u)=F(x)+u1g1(x)+u2g2(x)=-2x12-x22-4x1x2+6x1+1,5x2+u1 (2,5x1-x2–7)+ u2 (3x1+2,5x2-13). Получим уравнения седловой точки, применяя теорему Куна-Таккера: i=1;2 Объединим неравенства в систему А, а равенства в систему В: Система А: Система В: Перепишем систему А: 6-4x1-4x2+2,5u1+3u2 <0 1,5-4x1-2x2-u1+2,5u2 <0 2,5x1-x2–7³0 3x1+2,5x2–13³0 4)Введем новые ...
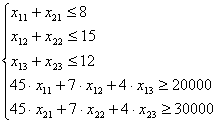
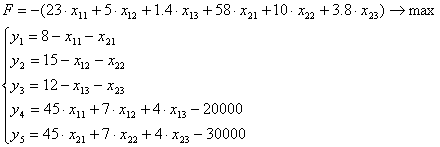
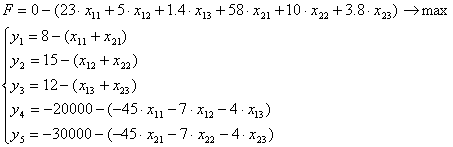
0 комментариев